解读Eviews回归结果（下）终于出现了，这次的讲解更贴近于考试使用。
如果你还没有读过上集，可以先观看计量经济学：解读Eviews回归结果（上）
先来看这个表
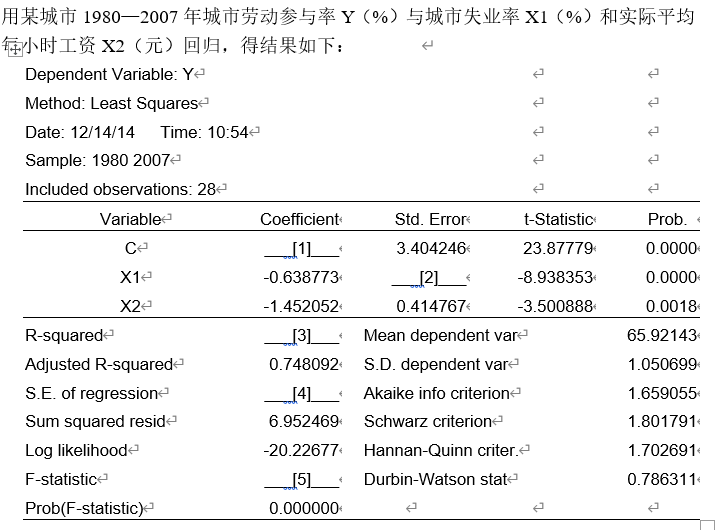尝试计算空白值
建议先手动算一下空白值，答案如下。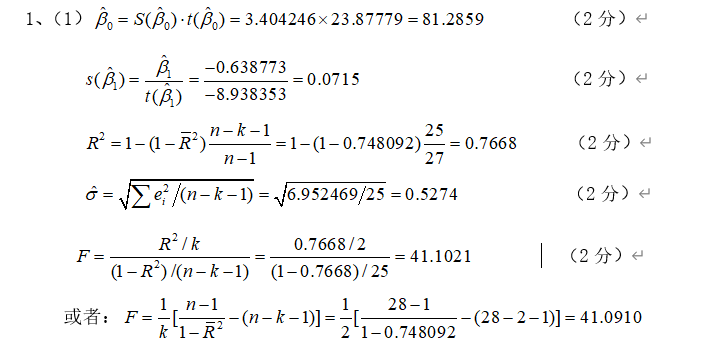
解答中的一些细节
表格中的上半部分的解答很简单，下半部分由$\bar{R^2}$，$n$，$k$，才得以算出。
其中这里的$n$就是样本容量（28），$k$是解释变量个数（其他地方和课本不一样，庞浩课本上默认把y也带进去了，所以第三行的公式你也可以写成：
$$R^{2}=1-\left(1-\bar{R}^{2}\right) \frac{n-k}{n-1}，k=3$$
解答第四行：
$$\hat{\sigma}=\sqrt{\sum e_{i}^{2} /(n-k-1)}$$
这里有两个地方值得注意，首先$S.E \space of \space regression$n是标准差，是要开方的，很容易忘记开方。其次在一元回归中：
$$\hat{\sigma}=\sqrt{\frac{\sum e_{i}^{2}} {n-2}}$$
在这里却变成了
$$\hat{\sigma}=\sqrt{\frac{\sum e_{i}^{2}} {n-k-1}}$$
因为一元线性回归是一个特例，$k=1$的特例，在计算多元线性回归的$S.E \space of \space regression$时，需注意使用通用的形式。
但是如果题目没有给$\bar{R^2}$，那么应该如何算R^2呢？
- 我们可以利用如下的公式计算。
$$(S.D \ dependent \ var)^2\cdot(n-1)=TSS$$
- 再利用
$$R^2=\frac{ESS}{TSS}=\frac{1-RSS}{TSS}$$
来计算$R^2$
值得注意的是：
- 有时候算出来会有误差，因为题目数字小数位数太少，给的不够精确。
- 题目小数点够多（比如本题），或者数字足够大，就可以放心用。
现在，你可以尝试用这种方法重新计算一下本题，还挺方便的。
再来看这个表
这是一个white检验，用来检验是否存在异方差，我们可以观察Obs R-squared 的显著情况来观察是否有异方差。
- p-value>0.1,显然不显著
所以并没有异方差。
再再来看这个表
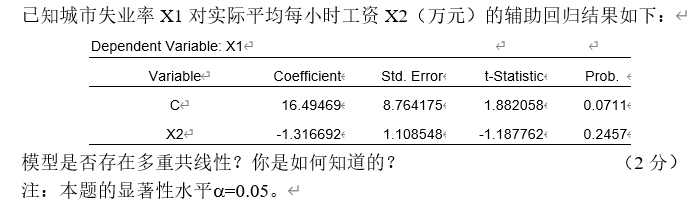所谓多重共线性，就是模型中含有的变量高度相关，事实上加进去跟没加一样（因为另一个变量足够解释模型了）。
所以我们新做一个模型，用$x_{1}$做因变量，$x_{2}$做自变量，看这个回归啊显著，显著了，就说明高度线性相关，有多重共线性。
那么很明显，$x_{2}$的 $p-value$不高，所以无多重共线性